Linear Regression Part 1

Supervised Learning 

• Regerssion : X is discrete or continuous → Y is continuous
• Classification : X is discrete or continuous → Y is discrete

 

 

Regression : Y is continuous 

• To predict the real-valued target y given a d-dimenstional vector x 
• X : independent variable, features, predictors
• Y : dependent variable, outcome
• Eg.,
  
  • 스마트폰 베터리 용량 → 스마트폰 지속 시간 
  • 연애 횟수 → 초콜릿 받은 양..

다르게 표현하면, from X to Y 를 가능하게 하는 function을 찾는 것이다. 따라서 Regerssion 모델을 학습하는 과정은 다음과 같이 나타낼 수 있다. 

 

Model Selection (모델 선택)

1.모델 선택

• 특정 모델 또는 모델 집합(및 하이퍼파라미터)을 선택
• 예: y=ax+by = ax + b

2. 목적 함수(오차 함수) 선택

• 모델의 성능을 평가할 수 있는 오차 함수(error function) 결정
• 예: 제곱 오차(Squared Error)

3. 학습(Learning)

• 학습 데이터 D_{train} 에 대해 오차 함수를 최소화하는 최적의 파라미터 (a, b) 를 찾음
• 즉, (a, b) 의 값을 조정하여 모델이 데이터를 잘 표현하도록 학습 🚀
• 에러를 최소화 하는 w 를 찾는 과정

 

Solving the Optimiazation Problem

Error function 은 주로 MSE(Mean-sqared error) 를 사용하여, 예측결과가 얼마나 정답과 일치하는지 판단한다. 

위에서 말했던 것 처럼 아래의 수식을 최소화 하는 방향으로 학습을 한다.  SLE(Squared loss error)를 이용하면 오차를 제곱하기에 작은 오차보다 큰 오차가 더 크게 반영되어 모델이 큰 오차를 줄이도록 학습하는 효과가 있다. 

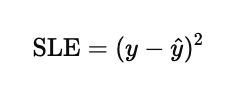
이러한 제곱함수는 Gradient Descent 등의 최적화 방법을 적용할 수 있다. 

경사하강 법은 반복적으로 에러 함수의 optimum 영역을 찾아가게 한다. 

 

어떤 함수 f(x)f(x) 가 주어졌을 때, 최소값을 찾으려면 기울기(Gradient, 미분 값) 가 0에 가까운 방향으로 이동해야 한다.
이 과정에서 반복적으로 업데이트를 수행하여 최적의 해를 찾는다.

수식적으로는,
현재의 파라미터 θ 를 기울기의 반대 방향으로 업데이트한다.

 

• θ : 최적화할 파라미터(예: 선형 회귀의 기울기, 절편 등)
• α: 학습률 (Learning Rate)
• ∇f(θ) : 손실 함수의 기울기(Gradient)

 

경사하강 방법 유형 

 

경사 하강법에는 업데이트 방식에 따라 3가지 종류가 있다.

1. 배치 경사 하강법(Batch Gradient Descent, BGD)

• 전체 데이터셋을 한 번에 사용하여 기울기를 계산하고, 가중치를 업데이트함.
• 장점:
  • 매우 안정적이고, 수렴 과정이 부드러움.
  • 전역 최적해(Global Optimum)에 도달 가능.
• 단점:
  • 데이터가 많을 경우 계산 비용이 큼(모든 데이터를 한 번에 사용).
  • 연산량이 많아 딥러닝에서는 잘 사용되지 않음.

---

 2. 확률적 경사 하강법(Stochastic Gradient Descent, SGD)

• 각 반복(iteration)마다 한 개의 샘플을 랜덤으로 선택하여 가중치를 업데이트함.
• 장점:
  • 연산량이 작아서 빠르게 학습 가능.
  • 지역 최적해(Local Optimum)에서 벗어날 가능성이 높음(노이즈가 있어서).
• 단점:
  • 불안정하고, 최적해 근처에서 계속 진동할 수 있음.
  • 최적의 수렴을 위해 학습률을 점진적으로 줄이는 기법 필요.

---

3. 미니배치 경사 하강법(Mini-batch Gradient Descent, MBGD)

• 전체 데이터셋을 작은 배치(batch)로 나누고, 각 배치에 대해 경사 하강을 수행.
•  
• 장점:
  • BGD보다 빠르고, SGD보다 안정적임.
  • GPU 병렬 연산에 적합하여 딥러닝에서 가장 많이 사용됨.
• 단점:
  • 배치 크기에 따라 성능이 달라질 수 있음.

 

 

Regularization

학습 데이터 포인트에 비해 만약 파라미터의 갯수가 overfitting 이 일어날 수 있다.

따라서 Regularization, 주로 모델의 가중치( w ) 크기를 줄이는 방식을 이용해 해결한다.

 

1. L1 정규화 (Lasso Regression)

• 비용 함수에 가중치의 절댓값( ∣w∣ )을 추가하여 가중치 값을 줄이는 방법.
• 불필요한 가중치를 완전히 0으로 만들어서 모델을 간소화함.
• 희소 모델(Sparse Model) 을 만들 때 유용.

L1 Regularization=λ∑∣w∣\text{L1 Regularization} = \lambda \sum |w|L1 Regularization=λ∑∣w∣

• 적용된 비용 함수:

Loss=∑(y−y^​)2+λ∑∣w∣

사용 예:

• 특성 선택(Feature Selection) → 중요하지 않은 특성(feature)의 가중치를 0으로 만듦.
• 희소 모델(Sparse Model) 적용 → 가중치가 0인 특성을 자동으로 제거.

---

2. L2 정규화 (Ridge Regression)

• 비용 함수에 가중치의 제곱( w2w^2w2 )을 추가하여 가중치가 너무 커지는 것을 방지.
• 모든 가중치가 0에 가까워지지만, 완전히 0이 되지는 않음.
• 과적합을 방지하고, 부드러운 모델을 만듦.

L2 Regularization=λ∑w2

• 적용된 비용 함수:

Loss=∑(y−y^​)2+λ∑w2

사용 예:

• 회귀 모델(Regression)에서 과적합 방지
• 가중치를 균등하게 줄이는 역할을 함.

---

3. Elastic Net (L1 + L2)

• L1 정규화와 L2 정규화를 동시에 적용한 방법.
• L1의 희소성(sparsity) + L2의 부드러움(smoothness) 을 결합.
• 적절한 균형을 맞추어 모델을 최적화.

Loss=∑(y−y^​)2+λ1​∑∣w∣+λ2​∑w2

사용 예:

• L1과 L2 각각의 단점을 보완한 정규화 방식.
• 특성 선택(Feature Selection) + 가중치 균형 조절이 필요한 경우.

---

Regularization의 효과

• 과적합 방지 → 모델이 너무 복잡해지는 것을 방지.
• 일반화 성능 향상 → 새로운 데이터에서도 성능을 유지.
• 희소성(Sparsity) 조절 → 불필요한 특성을 제거하여 효율적인 모델 생성.
• 모델이 너무 복잡해지는 것을 억제하여, 적절한 단순성과 성능 균형을 유지.